Bayesian Allocation Model and Non-Negative Matrix Factorization

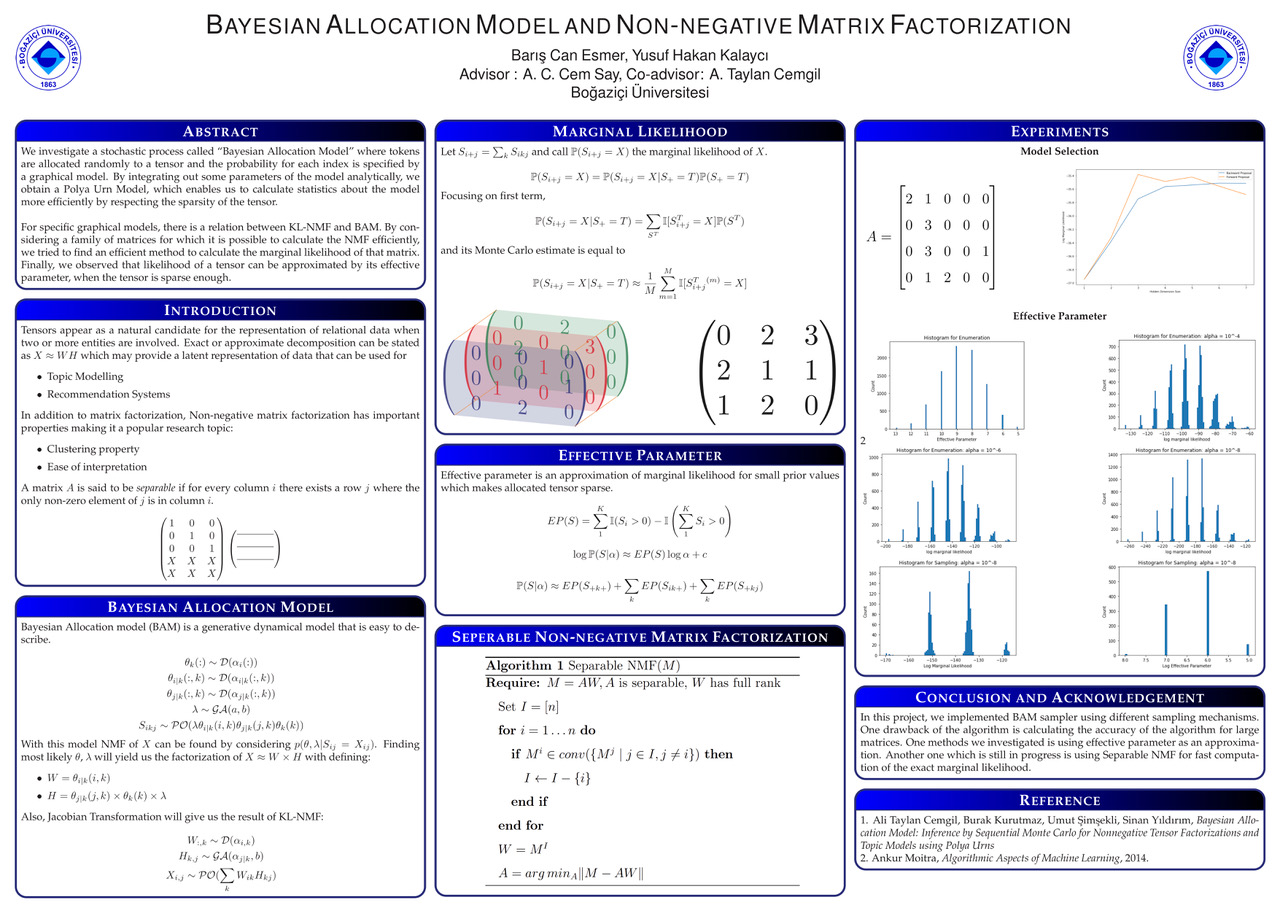
We investigate a stochastic process called ‘‘Bayesian Allocation Model’’ where tokens are allocated randomly to a tensor  and the probability for each index is specified by a graphical model. By integrating out some parameters of the model analytically, we obtain a Polya Urn Model, which enables us to calculate statistics about the model more efficiently by respecting the sparsity of the tensor.

For specific graphical models, there is a relation between KL-NMF and BAM. By considering a family of matrices for which it is possible to calculate the NMF efficiently, we tried to find an efficient method to calculate the marginal likelihood of that matrix. Finally, we observed that likelihood of a tensor can be approximated by its effective parameter, when the tensor is sparse enough.